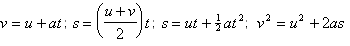Uniform linear acceleration
Introduction
This topic is about particles which move in a straight line and accelerate uniformly. Problems can vary enormously, so you have to have your wits about you. Problems can be broken down into three main categories:
Constant uniform acceleration
Remember what the following variables represent: t = the time ; a = the acceleration ; u = the initial speed ; v = the final speed ; s = the displacement from where the particle started. When the acceleration is negative, it is sometimes called a deceleration or retardation. For example, an acceleration of –3 ms-2 is the same as a deceleration (or retardation) of 3 ms-2.
• To answer this question, you will need to use the four key formulae intelligently.
This topic is about particles which move in a straight line and accelerate uniformly. Problems can vary enormously, so you have to have your wits about you. Problems can be broken down into three main categories:
- Constant uniform acceleration
- Time-speed graphs
- Problems involving two particles
Constant uniform acceleration
Remember what the following variables represent: t = the time ; a = the acceleration ; u = the initial speed ; v = the final speed ; s = the displacement from where the particle started. When the acceleration is negative, it is sometimes called a deceleration or retardation. For example, an acceleration of –3 ms-2 is the same as a deceleration (or retardation) of 3 ms-2.
• To answer this question, you will need to use the four key formulae intelligently.
• It is important to know the second of these equations off by heart; the others appear on Page 40 of The Mathematical Tables. Secondly, you may be asked to derive either of the last two equations from the first two. Practise this.
• These four formulae will be useful elsewhere (for example when doing Questions 3 and 4 on projectiles and connected particles).
Time-speed graphs
Remember that the above formulae may be used only while the acceleration is uniform. If a particle speeds up, but then travels at a constant speed, and then slows down, the above formulae cannot be used for the entire journey. In these cases we solve the problem by drawing a time-speed graph, with time as the horizontal axis.
There are four key points to remember about time-speed graphs:
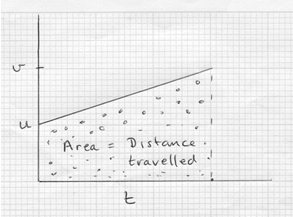
• The area between the graph and the time-axis represents the distance travelled.
• These four formulae will be useful elsewhere (for example when doing Questions 3 and 4 on projectiles and connected particles).
Time-speed graphs
Remember that the above formulae may be used only while the acceleration is uniform. If a particle speeds up, but then travels at a constant speed, and then slows down, the above formulae cannot be used for the entire journey. In these cases we solve the problem by drawing a time-speed graph, with time as the horizontal axis.
There are four key points to remember about time-speed graphs:
• The area between the graph and the time-axis represents the distance travelled.
• The slope of the graph represents the acceleration.
• If a particle starts from rest, then v = at [i.e. the final speed will be the product of the acceleration and the time.]
• If a particle starts from rest, then v = at [i.e. the final speed will be the product of the acceleration and the time.]
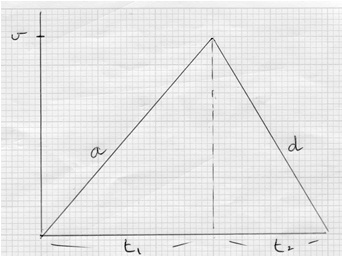
• If a particle accelerates from rest for time t1 with acceleration a and immediately decelerates to rest in time t2 with deceleration d, then t1:t2 = d:a
For example, if the acceleration is 6 ms-2 and the deceleration is 8 ms-2, then t1:t2 = d:a = 8:6 = 4:3 . It follows that of the time will be spent accelerating and of the time will be spent decelerating.
Problems involving two particles
• If particles P and Q set off together and later overtake each other, then overtaking will occur when Sp = Sq . If, however, P was 25 metres behind Q at the start, then when overtaking occurs,
Sp = Sq + 25
• If P and Q are a distance l apart and move towards each other, they will meet when Sp + Sq = l
• The greatest gap between particles P and Q occurs when vp = vq (because if their speeds are unequal then the gap is either increasing or decreasing)
• If particle A sets out and, two seconds later, particle B sets out in pursuit, then let t = the time which A spends on the road and t - 2 = the time which B spends on the road. (Students will often putt + 2 instead of t - 2.)
Common mistakes
Common mistakes made in doing this question are:
• Assuming that the particle starts from rest, even though this is not stated in the question.
• Using the formulae where they do not apply.
• Jumping into the question before giving it enough clear thought.
• Not drawing a clear time-speed graph.
• Letting u represent the speed at two different moments. For example, if a particle travels from a to b, a distance of 30 m in 4 seconds and then travels from b to c, a distance of 54 m in a further 3 seconds - how would you find the acceleration? You let u = the speed of the particle at a (not anywhere else!). Then you form an equation for the journey [ab] and another for the journey [ac] . These equations will be (using s = ut +½at2) : 30 = u(4) +½a(16) and 84 = u(7)+½a(49) . You solve these simultaneous equations to find a. NB: You do not form an equation for [bc], as the initial speed will not be the same u as in the first equation.
Problems involving two particles
• If particles P and Q set off together and later overtake each other, then overtaking will occur when Sp = Sq . If, however, P was 25 metres behind Q at the start, then when overtaking occurs,
Sp = Sq + 25
• If P and Q are a distance l apart and move towards each other, they will meet when Sp + Sq = l
• The greatest gap between particles P and Q occurs when vp = vq (because if their speeds are unequal then the gap is either increasing or decreasing)
• If particle A sets out and, two seconds later, particle B sets out in pursuit, then let t = the time which A spends on the road and t - 2 = the time which B spends on the road. (Students will often putt + 2 instead of t - 2.)
Common mistakes
Common mistakes made in doing this question are:
• Assuming that the particle starts from rest, even though this is not stated in the question.
• Using the formulae where they do not apply.
• Jumping into the question before giving it enough clear thought.
• Not drawing a clear time-speed graph.
• Letting u represent the speed at two different moments. For example, if a particle travels from a to b, a distance of 30 m in 4 seconds and then travels from b to c, a distance of 54 m in a further 3 seconds - how would you find the acceleration? You let u = the speed of the particle at a (not anywhere else!). Then you form an equation for the journey [ab] and another for the journey [ac] . These equations will be (using s = ut +½at2) : 30 = u(4) +½a(16) and 84 = u(7)+½a(49) . You solve these simultaneous equations to find a. NB: You do not form an equation for [bc], as the initial speed will not be the same u as in the first equation.
| q1._linear_acceleration.docx | |
| File Size: | 261 kb |
| File Type: | docx |