Relative Velocity
Introduction
This topic involves looking at the world from a different perspective. We are used to the idea of observing, say, two ships as they sail the seas. This way of looking down from above (like Zeus looking down from Mount Olympus) is sometimes called the Olympian View.
When we study relative velocity, we see life differently. We go on board one of the ships. We observe the other ship, as seen from our ship. The origin is no longer fixed, but moves wherever our ship moves. Looking at the situation in this way makes difficult problems easy to solve.
There are four main types of question:
Problems involving two particles
The key formula is vab=va -vb , where vab means the velocity of A as observed by B (i.e. the velocity of A relative to B).
• To answer this question, you must get away from thinking of problems from the Olympian view and get accustomed to looking at problems relatively. It takes time and practice - be patient.
• Draw plenty of diagrams - and make them clear, large and reasonably accurate.
• If you are told that a car is travelling at 30 km/h in a direction 20º North of West, you must learn how to convert this velocity into a vector in terms of i and j. Draw a diagram, and then use your Junior Cert Trigonometry to get the correct answer: it is -28.19i + 10.26j km/h.
• You also need to be able to do this process in reverse. Given, say, vab = 20i + 10j m/s, can you find the speed and direction of the particle. Again draw a diagram.
The speed =
This topic involves looking at the world from a different perspective. We are used to the idea of observing, say, two ships as they sail the seas. This way of looking down from above (like Zeus looking down from Mount Olympus) is sometimes called the Olympian View.
When we study relative velocity, we see life differently. We go on board one of the ships. We observe the other ship, as seen from our ship. The origin is no longer fixed, but moves wherever our ship moves. Looking at the situation in this way makes difficult problems easy to solve.
There are four main types of question:
- Problems involving two particles
- Road junctions
- Rivers, currents and winds
- Apparent velocity of wind
Problems involving two particles
The key formula is vab=va -vb , where vab means the velocity of A as observed by B (i.e. the velocity of A relative to B).
• To answer this question, you must get away from thinking of problems from the Olympian view and get accustomed to looking at problems relatively. It takes time and practice - be patient.
• Draw plenty of diagrams - and make them clear, large and reasonably accurate.
• If you are told that a car is travelling at 30 km/h in a direction 20º North of West, you must learn how to convert this velocity into a vector in terms of i and j. Draw a diagram, and then use your Junior Cert Trigonometry to get the correct answer: it is -28.19i + 10.26j km/h.
• You also need to be able to do this process in reverse. Given, say, vab = 20i + 10j m/s, can you find the speed and direction of the particle. Again draw a diagram.
The speed =
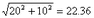
m/s.
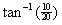
=26.565º North of East.
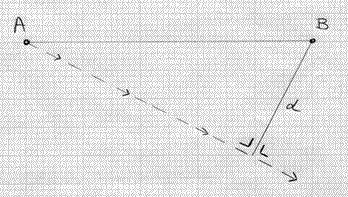
• The most common question asked is “Find the shortest distance between the particles”. Find the velocity of Arelative to B; draw a diagram; show where B is (B stays still, since wherever B goes, the origin goes) ; now show the path of A relative to B ; the shortest distance (d) is found by drawing a straight line from B, perpendicular to the relative path of A
• The most common question asked is “Find the shortest distance between the particles”. Find the velocity of Arelative to B; draw a diagram; show where B is (B stays still, since wherever B goes, the origin goes) ; now show the path of A relative to B ; the shortest distance (d) is found by drawing a straight line from B, perpendicular to the relative path of A
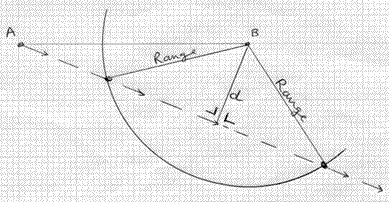
• If you are asked to find for how long are the particles within a certain range of each other, draw a circle around Band find the length of the chord (see diagram) using Pythagoras’ Theorem. The time taken will be got by
Road junctions
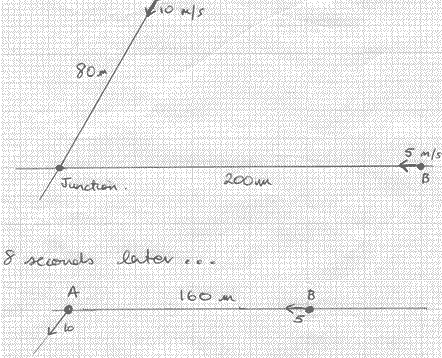
For example let’s say you are given the diagram below and asked what is the shortest distance between A and B in subsequent motion. It seems a very difficult problem. But what will happen if you wait 8 seconds until A is at the junction? Now here is the new situation and the problem is much easier. It can be solved using the steps outlined above.
For example let’s say you are given the diagram below and asked what is the shortest distance between A and B in subsequent motion. It seems a very difficult problem. But what will happen if you wait 8 seconds until A is at the junction? Now here is the new situation and the problem is much easier. It can be solved using the steps outlined above.
| q2._relative_velocity.doc | |
| File Size: | 555 kb |
| File Type: | doc |