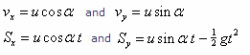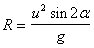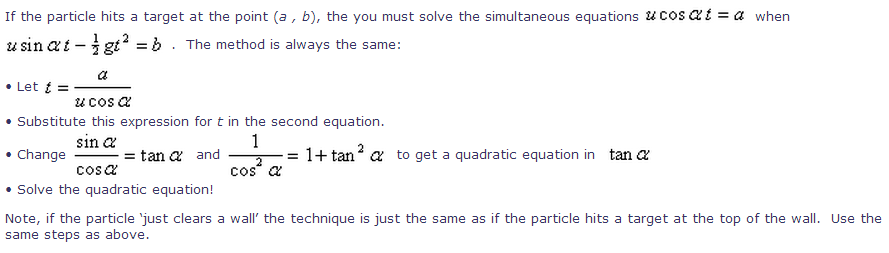PROJECTILES
Introduction
This topic is about objects which travel through the air under gravity. We analyse the problems by separating the x-direction (or i-direction) from the y-direction (or j-direction). It is important to distinguish between two very different vectors: the first is the position vector, which describes where the particle is at any time; the other is the velocity vector which describes the motion of the particle wherever it is. We are not interested in how the particle came to be flying through the air, we just want to know where the particle is and at what velocity is it travelling as it moves.
There are four main types of problem:
Projectiles on a horizontal plane
If the particle is projected on a horizontal plane with initial speed u at an angle to the plane, then its velocity and displacement in each direction will be:
This topic is about objects which travel through the air under gravity. We analyse the problems by separating the x-direction (or i-direction) from the y-direction (or j-direction). It is important to distinguish between two very different vectors: the first is the position vector, which describes where the particle is at any time; the other is the velocity vector which describes the motion of the particle wherever it is. We are not interested in how the particle came to be flying through the air, we just want to know where the particle is and at what velocity is it travelling as it moves.
There are four main types of problem:
- Projectiles on a horizontal plane
- Hitting a target
- Projectiles on an inclined plane
- Projectiles which bounce
Projectiles on a horizontal plane
If the particle is projected on a horizontal plane with initial speed u at an angle to the plane, then its velocity and displacement in each direction will be:
• If you want to find the ‘time of flight’, find t when Sy = 0
• If you want to find when the particle reaches its highest point, find t when vy = 0
• If you want to find the range, find Sx when Sy = 0 .
The general equation for the range is
• If you want to find when the particle reaches its highest point, find t when vy = 0
• If you want to find the range, find Sx when Sy = 0 .
The general equation for the range is
If you use this formula you must first derive it. Don’t produce it out of a hat!
• If you want to find the maximum height, find Sy when vy = 0 [The quickest way is to use the formula v2 = u2 + 2as ] The general equation for the maximum height is
• If you want to find the maximum height, find Sy when vy = 0 [The quickest way is to use the formula v2 = u2 + 2as ] The general equation for the maximum height is
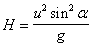
Again, show how to get this formula before you use it.
• A common question is to find the angle which gives maximum range and to find that range.
Hitting a Target
Projectiles on the Inclined Plane
| projectile-motion_en.jar | |
| File Size: | 551 kb |
| File Type: | jar |
| q3._projectiles.doc | |
| File Size: | 635 kb |
| File Type: | doc |